From Poker Theory to Trading Magic Cards

A few years ago, I was debating on a poker forum whether to call with Ace-King, when an unknown player pushes all-in on his first hand in a Sit and Go Heads Up (1 vs 1). Back then, my rationale was that if someone is bad enough to push all-in on his first hand (I won’t get into too many details, but this strategy is awful, regardless of your hand), I should wait for a better spot with better odds and lock an easy victory. Why risk my stack now with a 60% chance of winning, when I could wait until I have a 75%, 80% or even 100% chance of winning?

There was one answer I will never forget: “Man, what do you really want? To make your win percentage higher or to make more money?” I told him that raising my win percentage would mean more profits in the long run. He simply replied that I was wrong!

So how can losing 40% of my games make me more money than winning 100% of my Heads Up? Well, this is a little counter-intuitive. In order to answer the question properly, we must first understand a basic, yet crucial principle.

What is Expected Value?

Expected Value (EV) is the average value of the possible payoffs of an investment decision, taking into account the likelihood of each payoff. So, for example, if I’m playing a 100$ Sit and Go Heads Up (my investment equals 100$) there are two things that can happen: I lose the game and I’m down -100$ or I win the game and I’m up +100$.

Then, we must factor in the likelihood of each “payoff”. If I have a 60% chance of winning with AK, the EV would be calculated like this: (60% x 100$) + (40% x -100$) = +20$. So, what does that mean? It means that in the long run, if I play this exact scenario a million times, on average I’ll make 20$ each time. As long as my EV is positive, I’m making money.

Therefore, the higher my win percentage, the higher my EV. Where was I wrong then? I forgot something really important: time! If I call the first hand, it basically takes me two minutes to play my Sit and Go. If I wait until I find a better spot, it may take up to 15-20 minutes to actually win the game.

Let's illustrate this with two scenarios. In the first scenario, I call every time with my first hand being AK, and I win 60% of my games. Doing so, the games end within two minutes. For one hour of poker, I play 30 games and make +600$ (since our EV was +20$ per game, 30 x 20$). In the second scenario, I wait until I'm in a better spot where I have a guaranteed win (100%). In this case, it takes me 15 minutes to trap the guy and win. So now, I only have time to play four games per hour to net a 400$ profit.

I actually lose many more games in the first scenario, but I end up richer than in the second (and less tired too). Which one do you prefer?

How Does This Apply to Trading Magic Cards?

In fact, knowing about EV has a lot to do with trading cards. First of all, I think too many traders try too hard to find the best available opportunity (or the safest), when they could make much more profit by taking more risks, more often. In other words, it's more profitable to buy a card even if it still has a slight chance of losing value, then aim for the absolute floor price and hope for a 100% chance of profit. This was exactly the problem in my thinking when I was waiting for better than 60% odds with my AK.

Let's Get Concrete

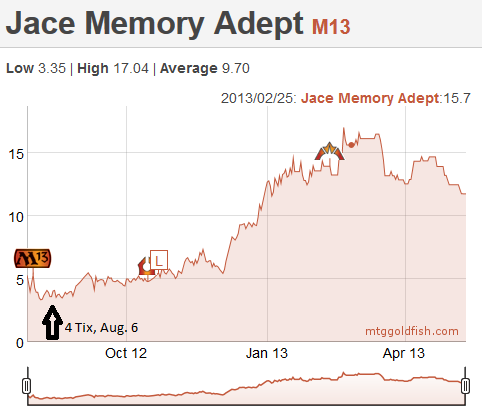
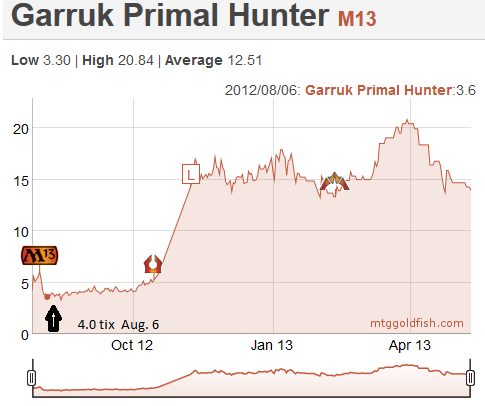
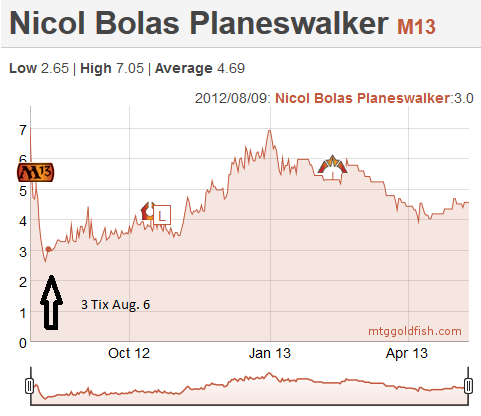
Let's consider three planewalkers that were reprinted in M13: Jace, Memory Adept, Garruk, Primal Hunter and Nicol Bolas, Planeswalker. In early August, I remember telling Sébastien that we should buy those in multiples. He posted on the forum and the general advice was to stay away, mostly because they were reprints. As we will see next week, the fear of reprints is another mistake we have learned not to make again. Given that we were pretty new to trading, we listened and mostly stayed away from these planewalkers.

Let's have a look at the charts for them, nine months later.

As you can see, Jace was 4 tix, Garruk was 4 and Bolas was 3, with many copies floating around on the classifieds. After nine months, you can see that Jace peaked at 17, Garruk reached 20.5, and Bolas 7. Sébastien and I ended up buying 20 copies of Nicol Bolas and 4-6 copies of Jace and Garruk. We sold everything for a nice profit. Still, if we had followed our original idea, we would be a lot richer today…

What If I Could Change the Way You Trade, Using EV?

What was the EV for these three calls? We obviously cannot calculate the exact EV for any call, because we cannot predict what will happen. But remember this: as a poker player, I was making money even though I did not know the hands of my opponents. I had to make assumptions. I ended up paying for my tuition, my wedding and my first car just based on such assumptions… So yeah, approximation works!

What if we go back in time, and do the math for these three specs. We are in August. There are rumors that we might be faced with another lockout in the NHL, and we are letting our frustration out on MTGO, buying Jaces and Garruks at 4 tix, and the unloved Nicol Bolas for 3.

We'll start by looking at a list of possible outcomes and trying to estimate the probability that each will occur:

• 50% -- Chance of losing a ticket (we rarely see PWs under 3 tix, even for reprints)
• 25% -- Chance of staying at their price (if they never show up in the meta, only redemption and casual play will support their price);
• 5% -- Chance of gaining 1 ticket (maybe from redemption and casual play)
• 5% -- Chance of gaining 2 tix (maybe from redemption and casual play)
• 5% -- Chance of gaining 3 tix (redemption and/or seeing play in one or two Standard decks)
• 5% -- Chance of gaining 4 tix (redemption and/or seeing play in one or two Standard decks)
• 5% -- Chance of gaining 10 tix (they play a significant role in the Standard metagame)

Now, let’s do the maths!

EV = (50% x -1)+(25% x 0) + (5% x 1) +(5% x 2) +(5% x 3) +(5% x 4)+ (5% x 10) = +0.40

So, on average, if I bought in August, I would make 0.4 tix per card. This assumes we are not concerned with Return on Investment (ROI), which I'll write an article on later. We could debate whether or not my assumptions were realistic, but I actually erred on the conservative side by granting a 75% probability of losing or selling at par. As a matter of fact, the real EV was much higher.

With such a conservative approach, the buying call on all three cards was supposed to be profitable in the long run. What I want you to realize is this: most traders are looking for the call, when they would make more money investing in lower +EV calls more frequently. Also, if you take a closer look at my calculations, I want to point out that the 5% chance the card breaks out and gains 10 tix balances out the whole 50% chance of losing a tix, given the 10:1 ratio. That means that it’s always better to look for cards with a slight chance to break out, even if there is some risk for their price to drop a little further down the road.

The Case of Baneslayer Angel

I remember a call I made on Baneslayer Angel during last Modern season. The card was getting popular, due to a W/G build played by Medvedev on MTGO. Seeing this, we decided to buy a bunch of them (200$), at an average cost of 7.75 tickets. As it turns out, the angel didn't see as much play as we expected, and we ended up selling our cards for an astonishing profit of 4 tix, after waiting a month.

This almost felt like a lost to me, given the amount of money that we had invested and the long waiting time. As of today, if I had to choose whether to invest or not in this spec again, I would do the exact same thing. The probability that the card could break the format was high enough to accept the risk and if I make the same investment over and over again, chances are I’ll make money.

On a side note, Baneslayer Angel sits pretty at 4.25 right now, so there is even less risk getting into this position now, in anticipation of the next season.

Good Decisions Can Still Result in Losses

Another thing that many people misunderstand about EV is that even if you have a positive EV, sometimes you’ll end up losing. This means that if you took a position in a card with +EV and lost money, you were still right to buy into it, and you should repeat the same process every other time in the future, in order to keep being profitable.

Every time you buy a card for which your calculations indicate a positive EV, you made the right decision, even if you end up losing money! When the rationale and the calculations support a buy, you should not determine if your decision was correct only based on the outcome.

Our contention is that this part of EV theory is the hardest to understand. People are generally outcome-oriented. They refrain from taking further risk based on one or two calls that cost them a few tickets. They end up thinking their reasoning was flawed or they blame their derailed intuition.

For instance, during Return to Ravnica spoilers, everyone was getting excited about G/B Zombies. It was supposed to be the next big thing, so we bought 100 copies of Woodland Cemetery. The deck died even before RTR's online release and Woodland's price dipped and stayed low for a long time. We will not stop buying lands because we lost on Woodland Cemeteries. Nor will we stop making calls based on the anticipated metagame. We know that over time, repeating similar calls will make us rich. Woodland was just a good call that turned sour.

The difference between a good and a bad trader is this: the good trader will not question his good decisions, even if some of them cost him money.

Should I Do the Maths Every Time?

This article is not only about doing math: it's really up to you to adhere to EV theories. Our intention is to share our thinking process when we decide whether we should take a position or not. When I phone Sébastien to talk about a new target, we are not just toying with percentages and calculations. In fact, EV's theory influences the way we talk about our specs. It often sounds like this: "I think this card is worth it because the probability of it going down is rather low, while there is a good chance for it to break out because..." Or: "This card has a good chance of not going up, but there is almost no downside. If it ever goes up, sky is the limit!"

On the Watch This Week

Watch for the dual lands in Legacy, as they all have their own alternate art now! We think they will all get awarded as prizes for MOCS seasons eventually. There are opportunities to make some money out of these, especially with Underground Sea and Tundra.

Jeff Goupil,
The Mathematician